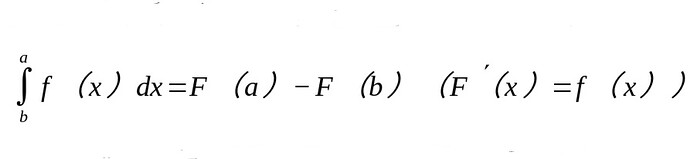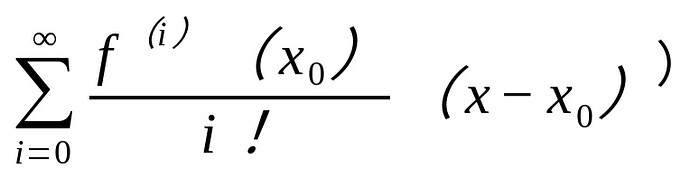编者按
1自然科学和社会科学不是割裂的,相反是相统一的。马克思主义的辩证法,可以在自然科学中起作用,而在一些时候,自然科学中也可以找到社会科学的奥秘。自然科学有真理,社会科学也有真理,那就是马列毛主义。2 马克思主义哲学决不是像中修所做的那样,割裂自然科学和社会科学的关系。它作为社会科学,是可以指导自然科学的发现的。作者所写,正是表明了辩证法的伟大胜利。不过本文的不足之处,在于没有揭露中修反动的教育,割裂了马克思主义哲学和数学这些自然科学的关系
3在数学这一自然科学中所体现的关系,比如函数中自变量对因变量的作用,由于因变量的取值又导致函数存在不同的值域,正是辩证的相互作用的关系的体现。但本文讨论的内容仍然不够通俗,所提到了“微积分”、“合数”的概念在没有解释的情况下,会令一部分读者难以理解。
4.毕达哥拉斯是勾股定理的发现者之一,支持地圆说,在当时的古希腊时期算比较进步的 。希帕索斯是毕达哥拉斯学派的人,由于发现了根号2,被毕达哥拉斯学派的人迫害至死。至于是不是毕达哥拉斯本人做的存疑,因为两人的年龄差距过大 。但是可以肯定的是,毕达哥拉斯学派在后期逐步走向了反动。
正如恩格斯所言:“数学:辩证的辅助工具和表达方式。(《自然辩证法》恩格斯)数学是辩证法在自然界的直接体现。数学处处充满着辩证法,数学就是辩证法的化身。因此,研究数学就是在研究自然辩证法,同时,研究自然辩证法也离不开数学。
一、计数
在人类社会的初期,就已经出现了计数,并由于这种计数的产生,人类社会出现了对于数字的概念。一切的开始是1、2、3……这些代表“有”的存在。而随着这种“有”的产生,无也随之出现,出现了0。
然而,数字是不能单独存在的,他必须要有算术,于是出现了加和减。随着人类在劳动中的不断发展,这种加减显然无法满足于当时社会的需要。于是,量变发生质变——乘除便出现了。
二、代数学和几何学中的辩证法现象
数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休。——华罗庚
随着人类劳动的发展,计数也随之发展。当这个发展产生质变时,代数学便产生了。
研究代数必不可少的就是研究方程,方程的出现是人类的一大进步。它的出现标志着人类从已知走向未知,从单纯的加减乘除计数走向了更加的复杂的未知数方程。除此之外,还为变化的数学——函数作了铺垫!
数学的发展不会是单方面的,人类的认识永远不会拘泥于单纯的数字,还有关于图形的认识。这种对于图形的研究就形成了几何学。
几何学和代数学是相互离不开的,从无理数的发现就可以清晰这一点。无理数是由一个“纯粹的”几何定理——勾股定理(或叫毕达哥拉斯定理,a^2+b^2=c^2)而来。
早期古希腊哲学的“万物皆数”,认为世间只有有限的有理数。但是,无限战胜有限,“无理”战胜“有理”是必然的,就如同“无理”的无产阶级战胜“有理”的资产阶级那般,是不可避免的。但是,反动派总归是不愿承认这般真理,他们总会用各种方式来阻扰真理的发现。逐渐走向反动的毕达哥拉斯学派将进步的希帕索斯杀死,企图“杀死”真理的无理数。但是真理就是真理,它永远是不随人的意志而转移的,真理最终总会被证明是正确的,无论反动派如何阻扰真理的证明,他们的阻扰永远都会失败。
纯粹的几何是不存在的,纯粹的代数亦然。代数即是几何,几何也是代数。解析几何就是这二者有机的结合!解析几何的出现,标志着代数和几何彻底合二为一,彻底走向了“合题”,这是辩证法的胜利!正如恩格斯所说:“数学的转折点是笛卡尔的变数,有了变数,辩证法进入了数学。”(《自然辩证法》恩格斯)
认识的发展是否定之否定式的,是不断的扬弃自身的过程。未知战胜已知,变化战胜静止,是必然的自然规律。所以,函数产生了!这是必然的,是不可避免的!函数的出现,是变量战胜了常量,是辩证法战胜了形而上学!
“有了变数,微分学和积分学也就立刻变成必要的了。”(《自然辩证法》恩格斯) 微积分的出现是辩证法在数学界向形而上学发动的“决战”,是彻底打破数学形而上学的最后一场战役。
三、微积分与辩证法
微积分的出现是数学史上惊天动地的大事,是辩证法在数学界的一次伟大的胜利!
微分和积分二者是无法分开的,正如矛盾双方一样,微分和积分也是一对矛盾的存在。他们二者是无限的“双生子”。一方是无穷小的微分(而不是所谓的无限趋近),另一方是无穷大的积分。二者作为无穷两端的存在,看上去相分离,但实际上仅是矛盾对立的两面。微积分基本公式(或叫牛顿—莱布尼茨公式,
)早已将二者的关系揭晓。但是直到19世纪,康托尔的集合论才真正的将无穷大和无穷小的对立统一关系表达出来。这确实表明了数学界中的形而上学影响过于强烈,亟需一场彻底的数学革命改造这一切!
无限和有限亦是无法分割之物,代数和微分、积分同样是对立统一的。微分通过不断的叠加(泰勒级数:
),量变产生质变变为了代数;同样的,代数通过不断的叠加,量变产生质变,变为了积分。
由此,微积分彻底将无穷小、无穷大、有限“三界”进行了统合。在辩证法和形而上学的决战中,辩证法再次赢得了胜利。